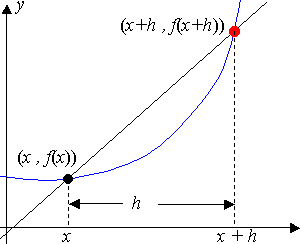
For a function f(x) the derivative from first principles is `lim_(h>0)(f(xh) f(x))/h` Using f(x) = sin 2x, the derivative is `lim_(h>0)(sin(2*(xh)) sin 2x)/h`Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Functions Line Equations Functions Arithmetic & Comp ConicWhen we have a question of calculating the derivative via first principles then it means that the idea is to drill down the definition of derivative via actual examples It also signifies that the student is beginning to learn differential calculus It is therefore much better to use techniques which rely on standard limits and don't rely on

07 Determining The Derivatives Using First Principles Mindset Learn
Derivative of e^2x by first principle
Derivative of e^2x by first principle- Let us find the derivative of e √2x with the first principle method Therefore, suppose f(x) = e √2x On using the first principle formula On rationalizingMathf(x) = e^{\sqrt{x}}\qquad f(x h) = e^{\sqrt{x h}}/math mathf'(x) = \displaystyle\lim_{h\to 0}\dfrac{f(x h) f(x)}{h}/math math=\displaystyle\lim




Grade 12 Differential Calculus First Principles Question Calculus
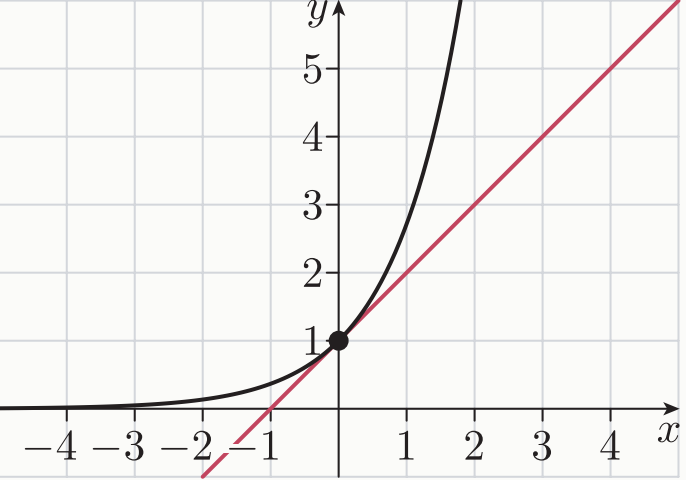
Differentiating Polynomials (a result from differentiation from first principles) We can show by differentiating from first principles, that d d x ( x n) = n x n − 1 For example, if y = x 3 then d y d x = 3 x 2 It follows that the point (2,8) on the cubic graph has a gradient of 12 We can find this by putting x = 2 into the derivativeUsing first principles, the derivative of the exponential function c^x can be simplified, however, determining the actual limit is best done by using a computerDerivative of ln (x) from First Principles
Example 19 Find the derivative of f from the first principle, where f is given by (i) f(x) = (2x 3)/(x − 2) Let f (x) = (2x 3)/(x − 2) We need to find Derivative of f(x) ie f' (x) We know that f'(x) = lim┬(h→0) f〖(x h) − f(x)〗/h Here, f (x) = (2x 3)/(x − 2) So,Given y = e^x From first principles we have dy/dx =`lim_(h>0)` (f(xh) f(x)) / h, therefore for y = e^x , dy/dx = `lim_(h>0)` (e^(xh) e^x ) / hDerivative of e 2x by first principle Music by adrian von ziegler I have been trying to differentiate the exponential function from first principles without the use of taylor s series or the derivative of its inverse function frac d dx ln x frac 1 x and ln e x x Find the derivative of f x 5x using first principles
Finding other derivatives by first principles If f(x) = g(x) h(x) , f'(x) = g'(x) h'(x) Examples If f(x) = x 2 2 , find f' (x) If f(x) = x 2 2x , find f' (x) If f(x) =x 2 2x 3, find f' (x) If f(x) = x 3 2x 2 3x 4, find f' (x) Derivative of a function f(x) from first principle is given by – {where h is a very small positive number} ∴ derivative of f(x) = √(2x 2 1) is given as – As the above limit can't be evaluated by putting the value of h because it takes 0/0 (indeterminate form) ∴ multiplying denominator and numerator by \(\sqrt{2(xh)^21}\sqrt{2x1 I know the first principle, f ′ ( a) = lim x → a f ( x) − f ( a) x − a However, I don't know what to do next Help derivatives Share edited Nov 16 '14 at 1706 user asked Nov 16 '14 at 1652




1 I




Find The Derivative Of Cube Root Of Sin X Using First Principle Brainly In
f (x) = (2x − 1) You want the derivative of f to the power − 1 2 Chain rule − 1 22(2x − 1)− 1 2−1 The factor 2 comes from the derivative of f itself Answer linkShare It On Facebook Twitter Email 1 Answer 1 vote answered Feb 5 by Tajinderbir (370k points) selected Feb 5 by Raadhi Best answer Let f(x) = sin 2x ∴ By first principle# Apply 1st principle formula#(ab) to the power 3 formula# limit concept



Differentiation From First Principles Free Homework Help



Chain Rule In Differentiation Of E X From First Principles The Student Room
Ex 132, 4 Find the derivative of the following functions from first principle (i) x3 – 27 Let f(x) = x3 – 27 We need to find Derivative of f(x) ie f' (x) We know that f'(x) = lim┬(h→0) f〖(x h) − f(x)〗/h f (x) = x3 – 27 f (x h) = (x h)3 – 27 Putting valuesLet y = 2x(1) Let ∆x be a small change in x Let ∆y be the corresponding change in y Then y ∆ y = 2 (x ∆ x) = 2x 2∆x (2) (2)(1Derivative by first principle refers to using algebra to find a general expression for the slope of a curve It is also known as the delta method The derivative is a measure of the instantaneous rate of change, which is equal to f ′ (x) = lim h → 0 f (x h) − f (x) h f'(x) = \lim_{h \rightarrow 0 } \frac{ f(xh) f(x) } { h }




Differentiate E 2x 1 With Respect To X By Using First Principle
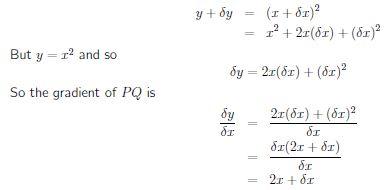



Differentiation From First Principles A Level Revision
Stack Exchange network consists of 177 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack ExchangeI suppose it's allowed as "first principles" to use the definition of derivative d d x tan (x 2) = lim h → 0 tan ((x h) 2) − tan (x 2) h Hopefully it's also allowed as "first principles" to use the trigonometric identity that tan α = sin α cos α Notice that, for any a, b, tan a − tan b = sin a cos Show activity on this post I am trying to differentiate 2 x from first principles This is what I have so far f ′ ( x) = lim h → 0 f ( x h) − f ( x) h d 2 x d x = lim h → 0 2 x h − 2 x h = lim h → 0 2 x ( 2 h − 1) h From that point on, as the limit is of type 0/0, I was thinking of using L'Hôpital's rule, but this gives



1




Differential Calculus Differentiation Using First Principle Differential Calculus Calculus First Principle
Derivative of e^x using first principle Differentiation of e^x by first principle we have offline and online coaching for JEE Main, JEE Advanced, NEET, Cla Find from first principle, the derivative of 2x^2x with respect to x Questions in other subjects Computers and Technology, 17 In the main function, define four variables of type int, named first, second, third, and total write a function named getdata that asks the user to input three integers and storDerivative from First Principles Derivative from First Principles Watch later Share Copy link Info Shopping Tap to unmute If playback doesn't begin shortly, try restarting your




Example 19 Find Derivative From First Principle I F X 2x 3




Differentiate E To The Power Root 2x By Using First Principle Maths Continuity And Differentiability Meritnation Com
DIFFERENTIATION FROM FIRST PRINCIPLES Given y = f(x) its derivative, or rate of change of y with respect to x is defined as Example 1 Differentiate 2x 2x from first principles Misc 1 Find the derivative of the following functions from first principle –x Let f (x) = – x We need to find derivative of f(x) ie f' (x) We know that f'(x) = lim┬(h→0) 𝑓〖(𝑥 ℎ) − 𝑓(𝑥)〗/ℎ Here, f (x) = – x So, f (x h) = – (x h) Putting values f' (x) = lim┬(h I am able to find derivatives of $\sin x$ and $\sin 2x$ using first principle (Using the formula for $\sin(A)\sin(B)$ and subsequently using $\lim_{x\rightarrow 0}$ $\frac{\sin x}{x}$ = 1 But I am getting stuck in trying to find Derivative of $\sin(x^2)$ using the same




Find The Derivatives By Using First Principle A 2x Gauthmath




Derivative Of Tan 2x E Sinx By Using First Principle Method Maths Limits And Derivatives Meritnation Com
Click here👆to get an answer to your question ️ Differentiate the following from first principle tan(2x 1)In this video learn how to find the derivative of a function by first principle with makes u comfortable and easier in approachi hope u will get benefited bDifferentiate sec x by first principle Easy Video Explanation Answer Let f (x) = sec x Find the derivative of c o s 2 x, by using first principle of derivatives Medium View solution If




I Ve Always Seen The Derivative Of E X Found Via The Chain Rule How Can I Find It Using The Power Rule Quora



Essential Mathematics Calculus
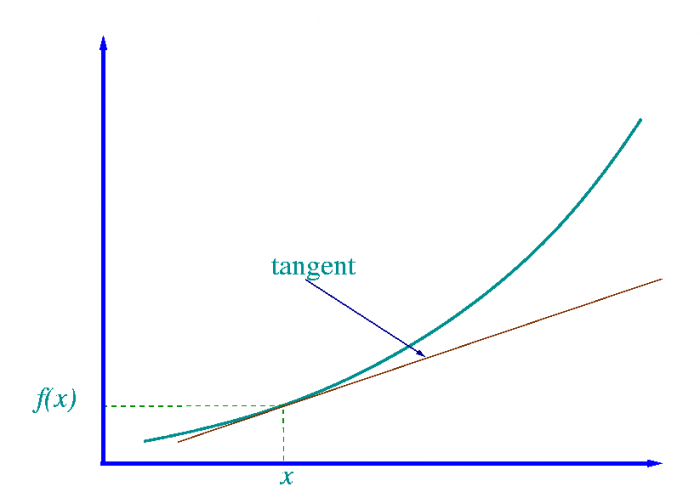
62 Differentiation from first principles (EMCH6) We know that the gradient of the tangent to a curve with equation y = f ( x) at x = a can be determine using the formula Gradient at a point = lim h → 0 f ( a h) − f ( a) h We can use this formula to determine an expression that describes the gradient of the graph (or the gradient of the tangentDerivative of e^x from first principle (DERIVATIVE USING FIRST PRINCIPLE) DIFFERENTIATION CLASS 12 Watch later differentiate f (x)=x^3x^21/x with respect to x A particle moves along a straight line such that its displacement s at any time t is zero is s=t^36t^23t4 meters, t being in second The velocity when acceleration is zero is Find the derivative of tan x at x = 0 Find the derivative of the function f (x) = 15x and x = 3




Differentiation Archives Graphic Education




Grade 12 Differential Calculus First Principles Question Calculus
First principle of e^2x I class 11 XI, ncert I cbse I differentiation I abinitio, delta method by deepak mittalThe process of determining the derivative ofDerivative Of E^2x By First Principle Collection Review the Derivative Of E^2x By First Principle 21 pics and Derivative Of E^x^2 By First Principle and also Ece çelik GoFind the derivative of sin 2x by first principle derivatives;
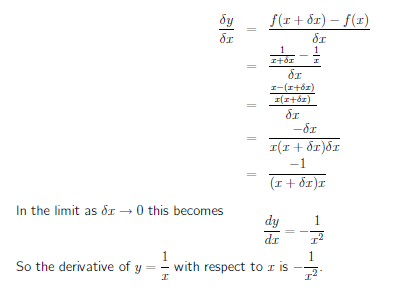



Differentiation From First Principles A Level Revision




07 Determining The Derivatives Using First Principles Mindset Learn
Find the derivative of y=e^x using first principles 1 Educator answer Math Latest answer posted at 1637 PM Find the derivative of xsinx by first principle 1 Educator answerGradient at a point = lim h → 0f(a h) − f(a) h We can use this formula to determine an expression that describes the gradient of the graph (or the gradient of the tangent to the graph) at any point on the graph This expression (or gradient function) is called the derivativeDifferentiate the following from first principle tan 2x > 11th > Maths > Limits and Derivatives > Derivative of Trigonometric Functions > Differentiate the following




Find The Derivatives By Using First Principle A 2x Gauthmath




Differentiate E 2x With Respect To X From First Principles
DIFFERENTIATION from first principles Created by T Madas Created by T Madas Question 1 (**) f x x( ) = 2, x∈ Use the formal definition of the derivative as a limit, to show that




Derivative Calculator Wolfram Alpha




Proof The Derivative Of 𝑒ˣ Is 𝑒ˣ Video Khan Academy



Differentiate The Functions From The First Principles E Cos X Sarthaks Econnect Largest Online Education Community
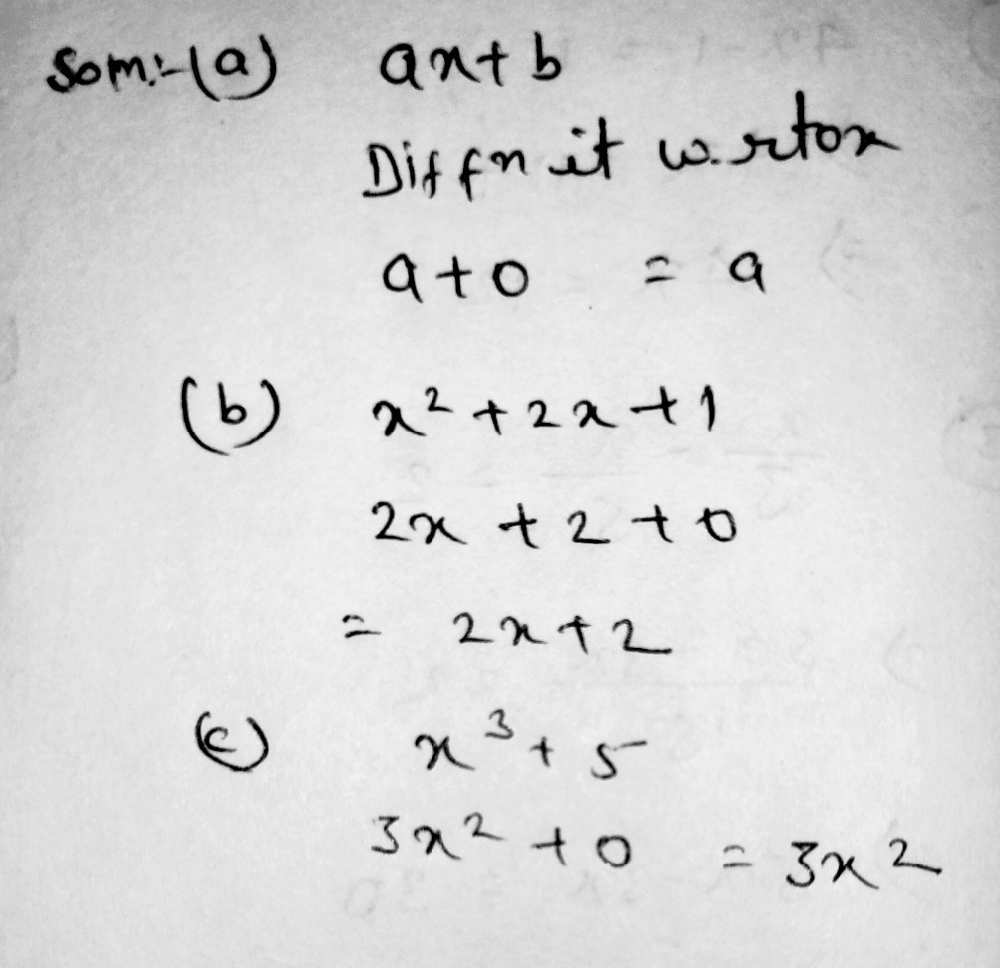



Ta S Foundations Of Mathematics Exercise 14 1 1 Gauthmath



Www Nuigalway Ie Media Publicsub Sites Engineering Files Differential Calculus 2 Pdf




The Derivative Of F X E 2x Is




Differentiate E 3x From First Principles




Answered 2x By Applying The Derivatives From Bartleby




Derivative Of E X By First Principles Brainly In




Differentiate The Following From First Principle Sin 2x 3



Www Calvin Edu Scofield Courses M162 S07 Frameworks Allframeworks Pdf




Ex 13 2 10 Find Derivative Of Cos X From First Principle Teachoo




C By Using The Derivatives From First Principle Chegg Com



Differentiate The Following Functions From First Principles E 2x Sarthaks Econnect Largest Online Education Community



Http Www Stat Wisc Edu Ifischer Calculus Pdf




Finding The Derivative Of Sec 2 X Video Lesson Transcript Study Com



Bestmaths




Differentiation



What Is The Differentiation Of E X By The First Principle Quora




E Mc 2 Deriving The Equation From First Principles Advanced




Proof The Derivative Of 𝑒ˣ Is 𝑒ˣ Video Khan Academy




Differentiate E 2x 1 With Respect To X By Using First Principle Youtube




Derivative Of 𝑒ˣ Video Khan Academy
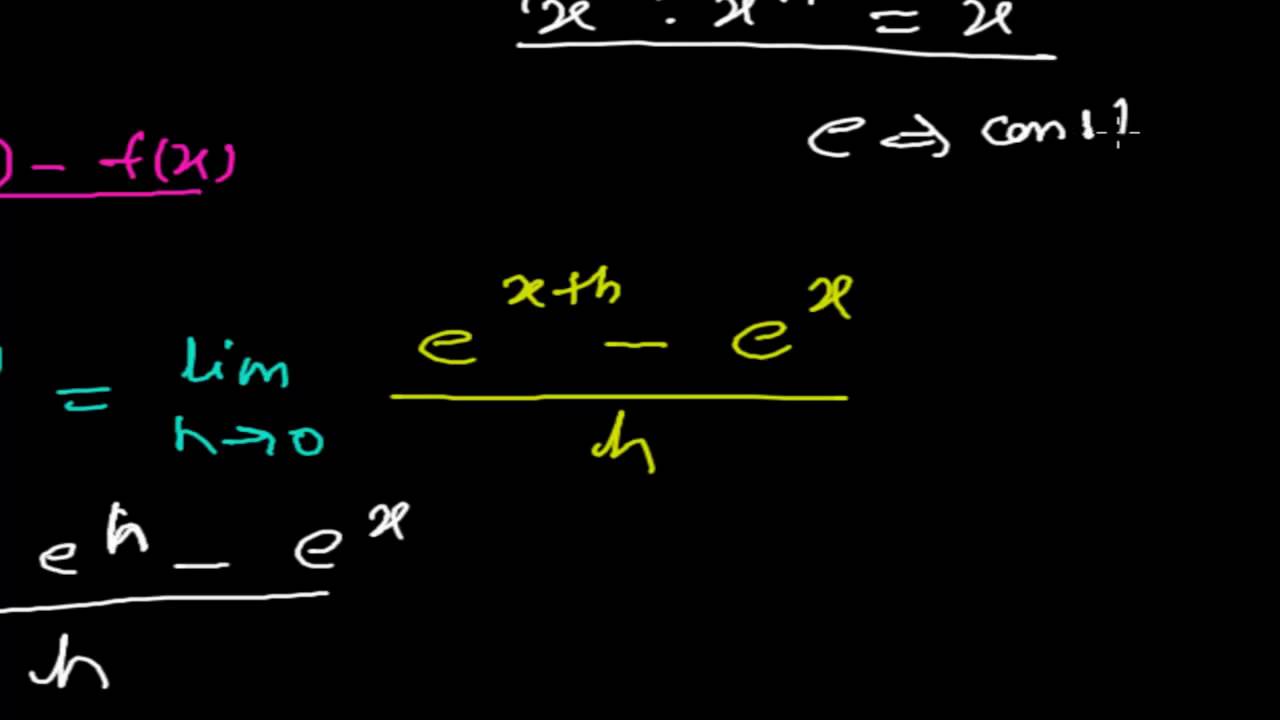



Derivative Calculus Proof Derivative Of E To The Power X E To The Power X By First Principle Youtube



1




How To Use First Principles To Find The Derivative Of Math X X Math Quora




Answered 2x Lerivatives From First Principle Bartleby



What Is The Derivative Of Math E 2x Math Quora




Differentiate E 2x 1 With Respect To X By Using First Principle



Derivative Of E X From First Principles Youtube




Derivative Of E X From First Principles Youtube



3 The Derivative From First Principles




Product Rule Wikipedia



What Is The Derivative Of E 2x Science Trends
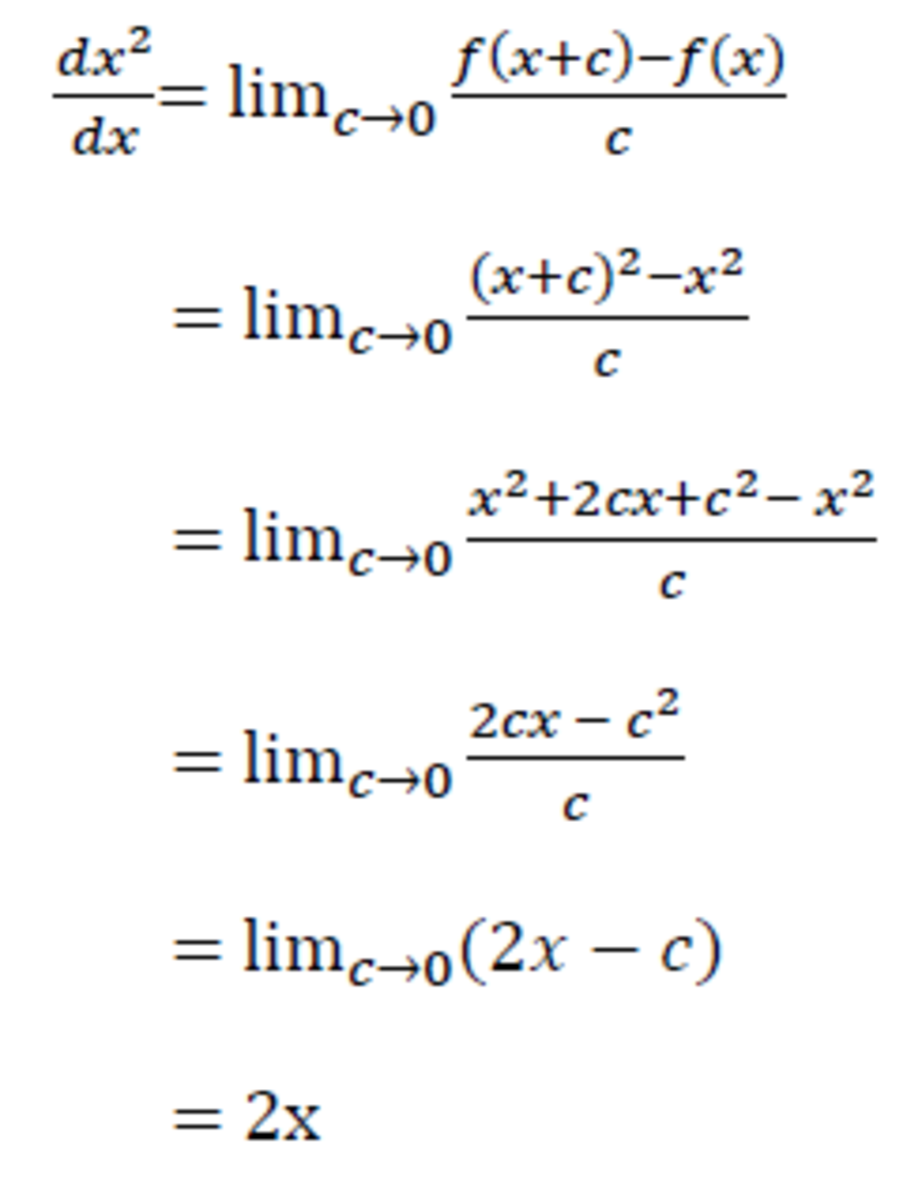



How To Differentiate From First Principles Owlcation




11x1 T08 02 First Principles




Find The Derivative Of E Sqrt X From The First Principle Youtube




Ex 13 2 4 Find Derivative From First Principle I X3 27



Partial Derivatives



Differentiate E 2x W R T X From First Principles Sarthaks Econnect Largest Online Education Community




Differentiation First Principles Ppt Video Online Download
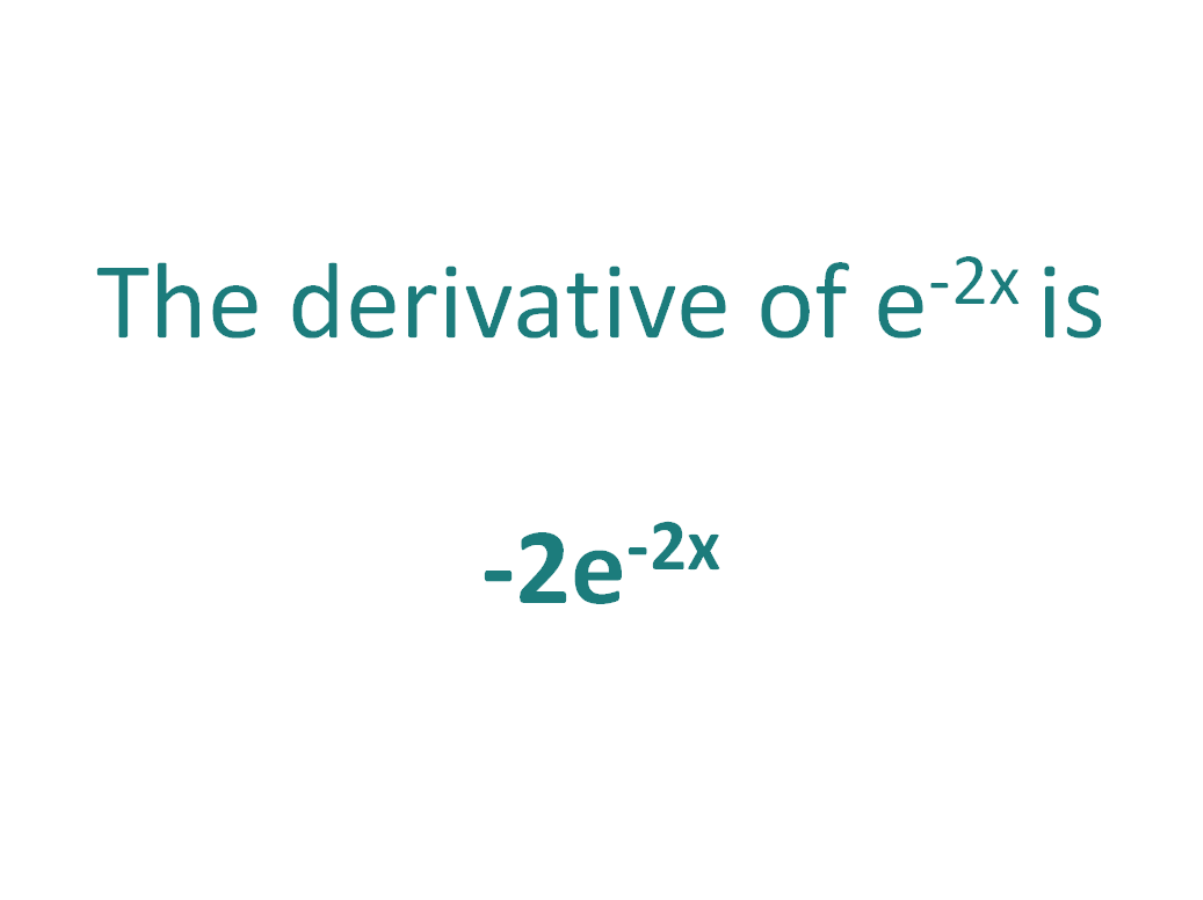



The Derivative Of E 2x Derivativeit




Analysis Of Errors In Derivatives Of Trigonometric Functions International Journal Of Stem Education Full Text




Find The Derivative Of Tanx By First Principle Mathematics Topperlearning Com Iyyne
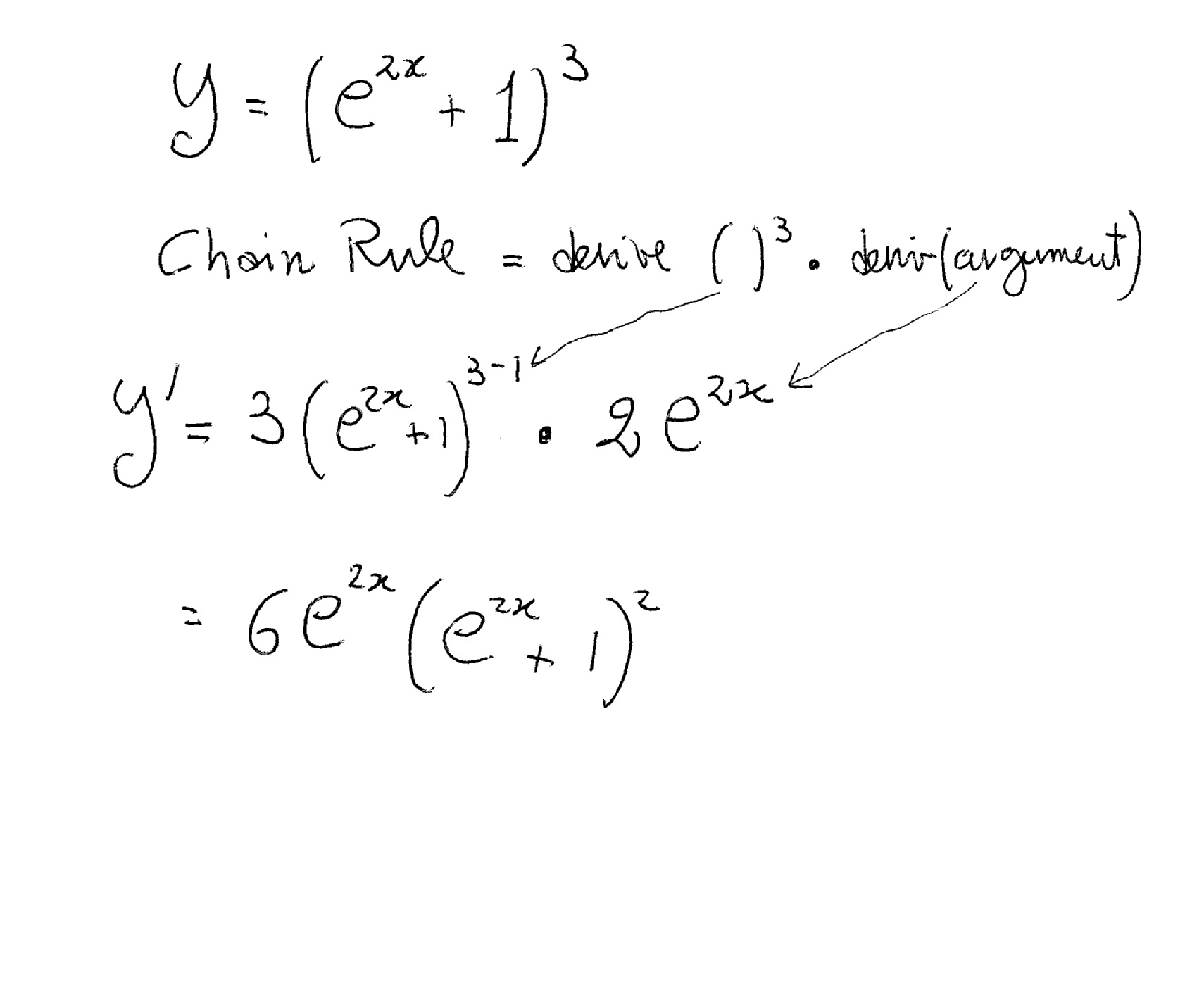



What Is The Derivative Of This Y E 2x 1 3 Socratic
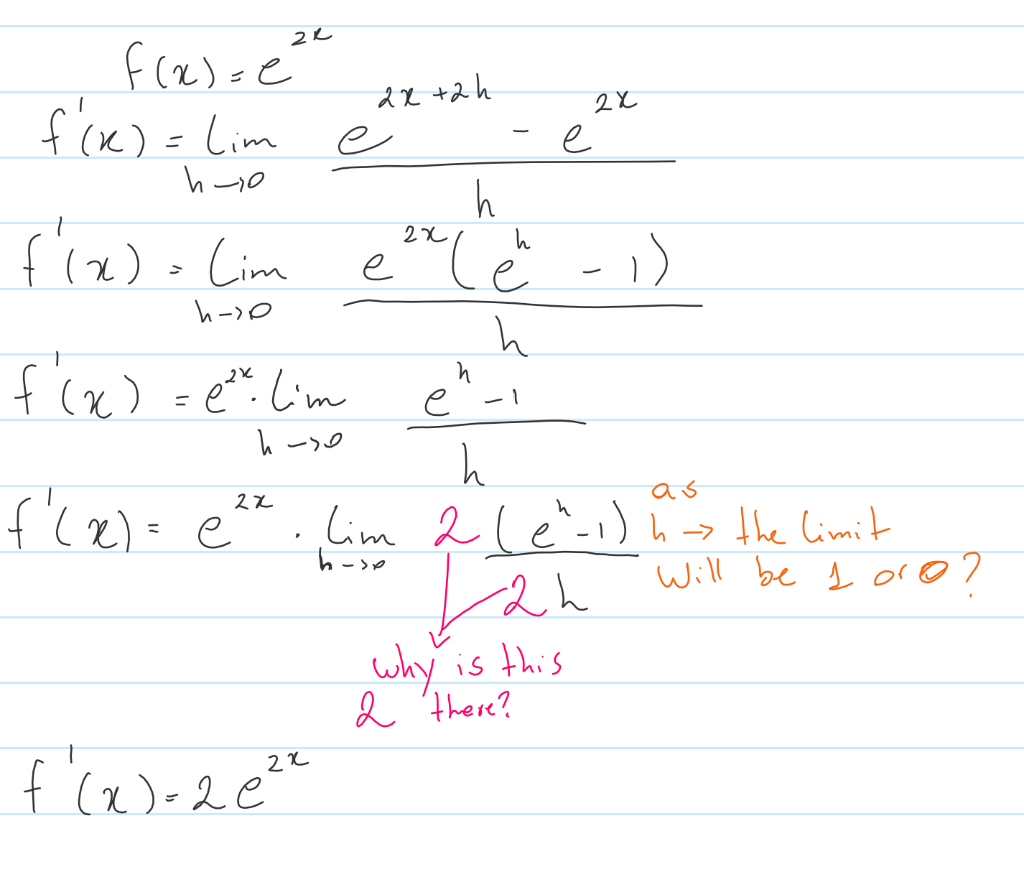



Find The Derivative Of E2x By The First Principle I Chegg Com




Find The Derivative Of Sin 2x From First Principle Cbse Class 11 Learn Cbse Forum



3 The Derivative From First Principles




1 A To Find The 10 Use The First Principle Of Chegg Com



Math Scene Derivatives Lesson 4 Derivatives Of Exponential And Trig Functions
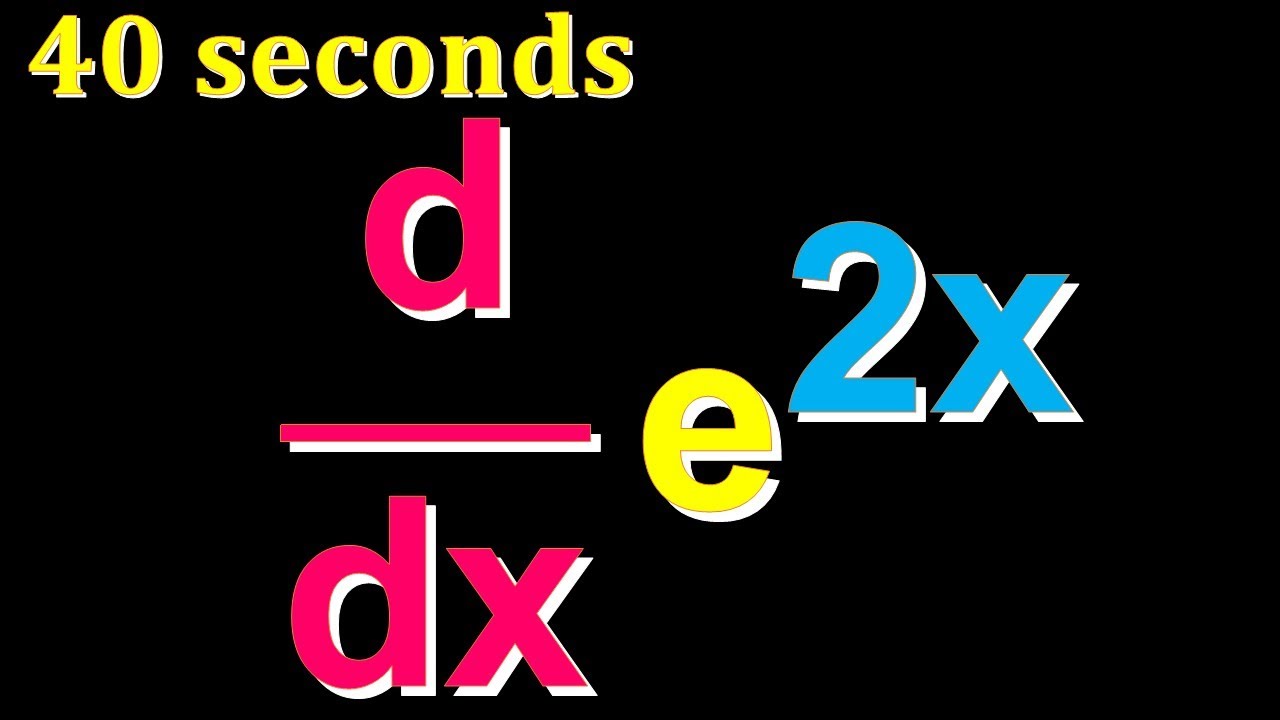



Derivative E 2x In 40 Seconds Derivative Of E 3x In The Description Youtube




Differentiation From First Principles Ppt Download



Differentiate The Functions From The First Principle E 2x Sarthaks Econnect Largest Online Education Community
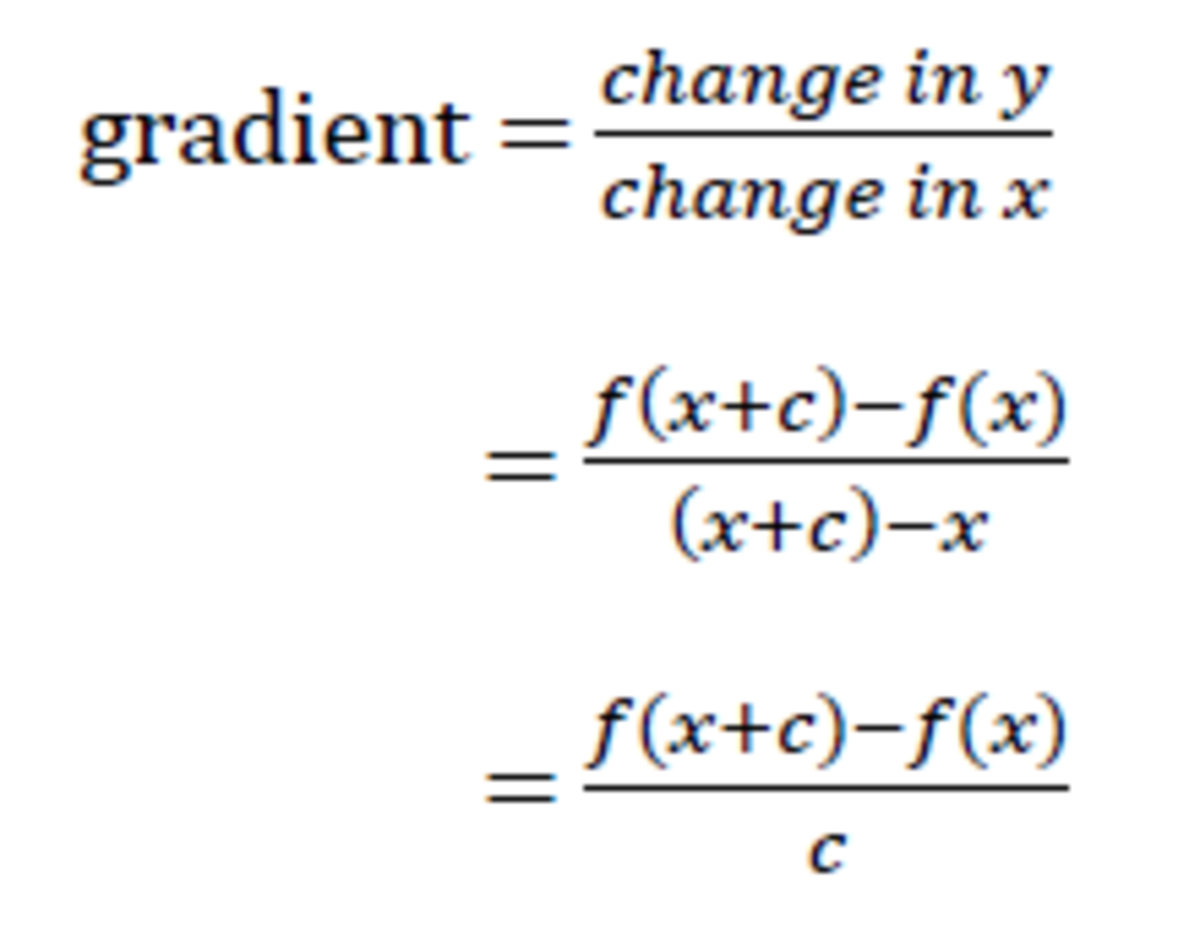



How To Differentiate From First Principles Owlcation



3 The Derivative From First Principles




6 2 Differentiation From First Principles Differential Calculus Siyavula




Differentiate The Following From First Principle Tan 2x 1



1



Jf5vbyadxkm7jm
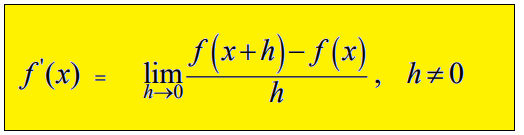



Differentiation From First Principles
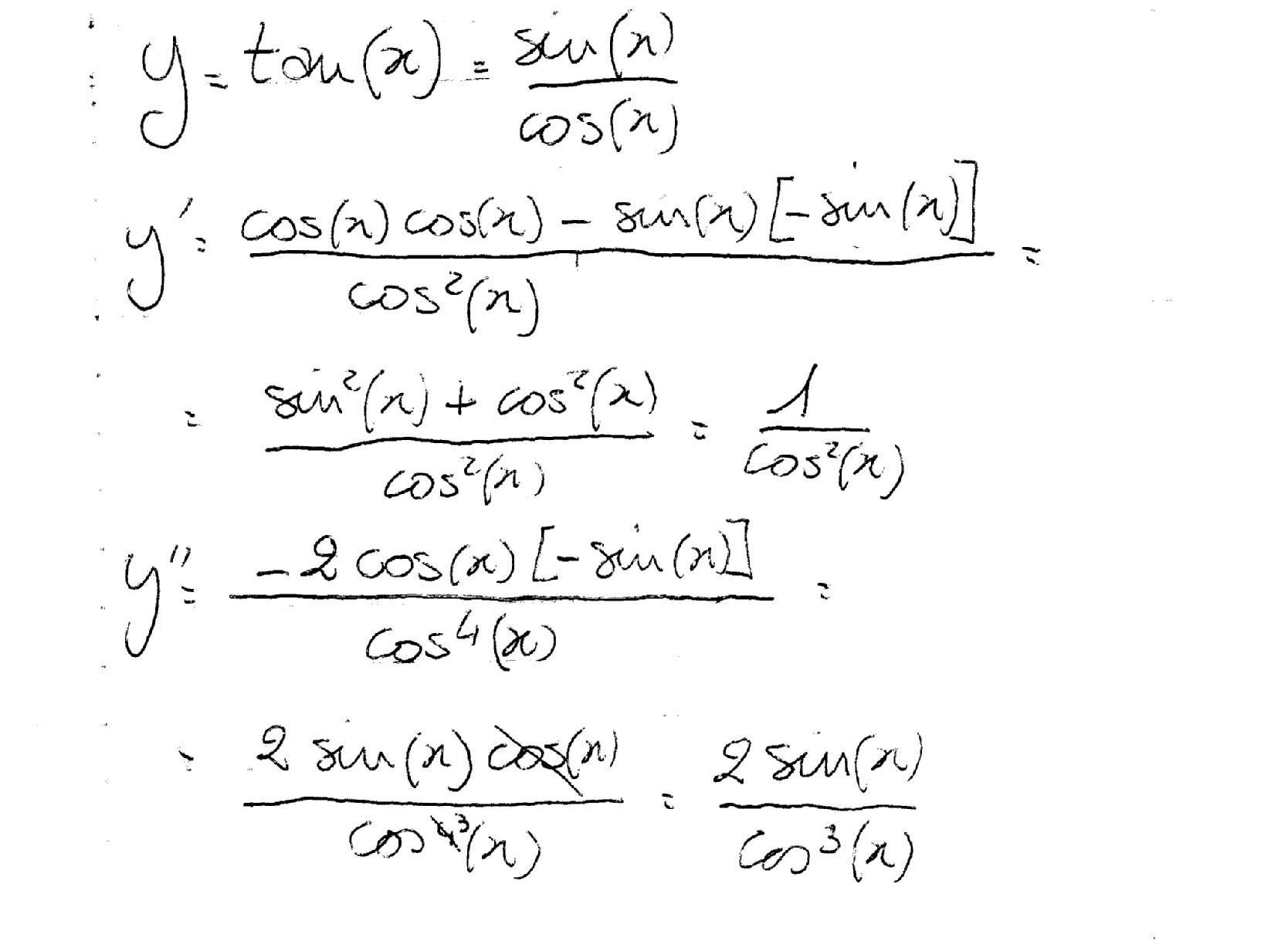



What Is The 2nd Derivative Of Y Tanx Socratic



Find The Derivative Of Sin 2x From First Principle Mathematics Topperlearning Com Rygujflcc




Differentiate Xe X From First Principles
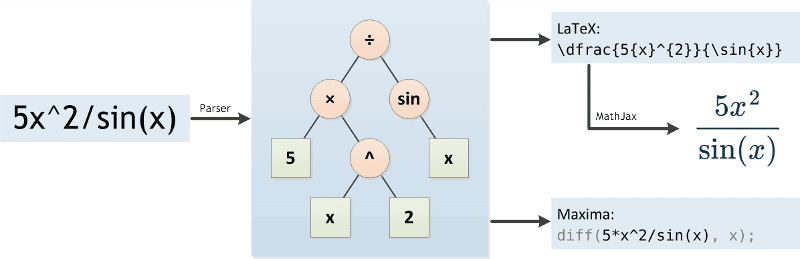



Derivative Calculator With Steps




Rd Sharma Solutions For Class 12 Maths Updated For 21 22 Chapter 11 Differentiation




Cbse Class 12 Differentiation Of Log Base E X And Log Base A X From First Principles In Hindi Offered By Unacademy




Tutorial Chapter 2 Differentiation Studocu



2




First Principle Of Derivatives Tutorsonnet
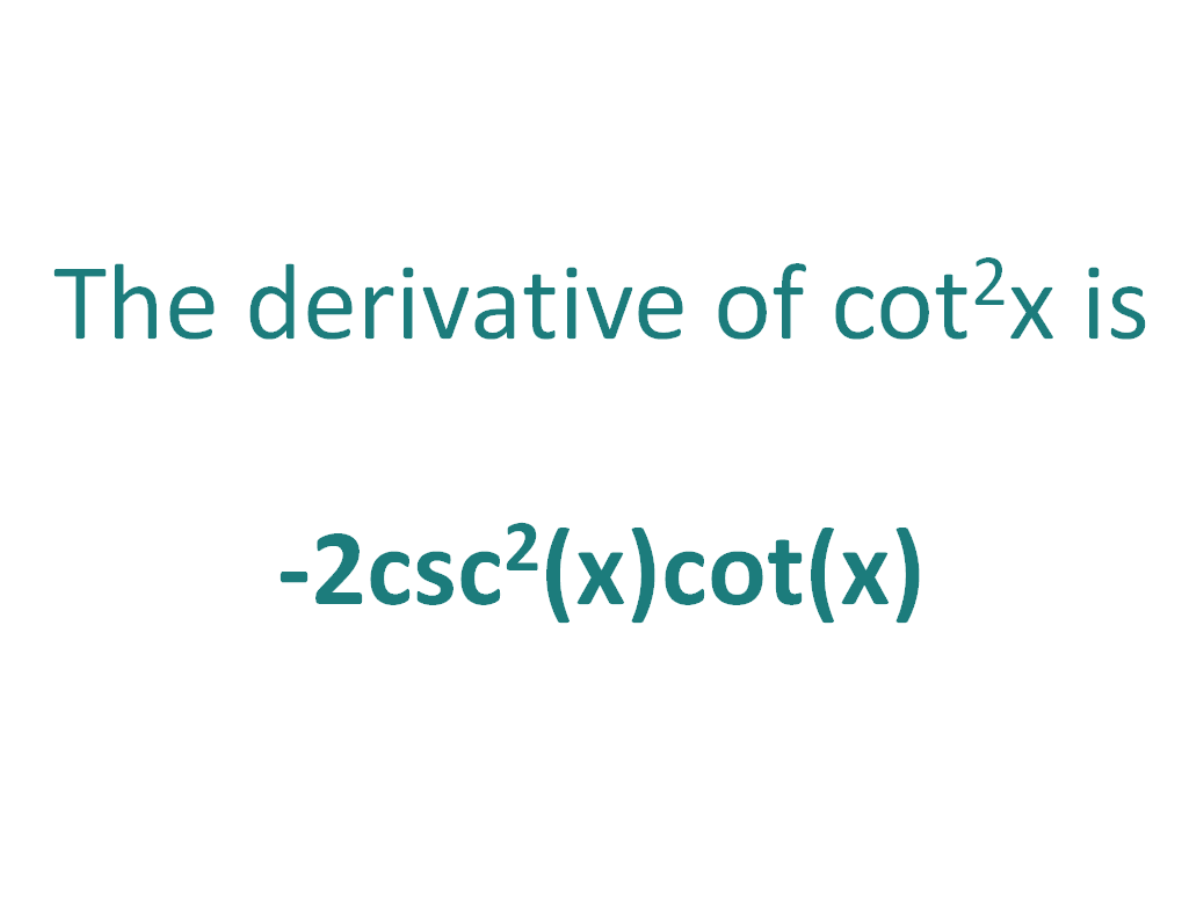



The Derivative Of Cot 2x Derivativeit




Differentiating From First Principles Youtube




Rd Sharma Solutions For Class 11 Maths Updated For 21 22 Chapter 30 Derivatives Download Free Pdf



3




Find The Derivative Of F From The First Principles Where F Is Given By F X 2x 3x 2




Example 19 Find Derivative From First Principle I F X 2x 3




1 Differentiate From First Principles A Y 4x 2 7 Chegg Com



Math Scene Derivatives Lesson 4 Derivatives Of Exponential And Trig Functions




Find The Derivative Of Cos 2x 3 From First Principle Brainly In




The Limit Does Not Exist Dr Stone Maths



Http Www Madasmaths Com Archive Maths Booklets Advanced Topics Laplace Transforms Pdf




Find The Derivative Of The Following Functions From First Principle X 1 X 2 Mathematics Shaalaa Com




Chapter 2 Derivatives 1 Using First Principle Find Chegg Com




Differential Calculus Wikipedia




Find The Derivative From First Principle Secx 2 Maths Limits And Derivatives Meritnation Com


